6-3 유의수준
모집단에 대해 어떤 주장이 맞는가를 판단하기 위해서는 표본을 얻어 표본으로부터 구해진 결과를 이용해야 한다는 것은 당연하다.
그러나, 모집단 전체에 대해서는 영원히 모르는 것이기 때문에, 가설 검증의 과정을 거쳐 의사결정을 할 때 과오(오류)를 범할 수도 있을 것이다.
왜냐하면(하나님만이 알고 있을) 모집단 전체에 대한 값이 어떻다는 판단을 하는 데 표본을 통하여 사람이 판단하기 때문이다.
물론 이 또한 정확하게 안다는 것은 불가능 한 것이 아니겠는가.
따라서 신뢰도...%에 얼마에서 얼마까지라고 구간으로 추정 할 수 밖에 없는 것 아닌가.
여기에서 문제는 신뢰도를 어떻게 해야 하는가이다.
이 신뢰도에 따라 가설이 옳다 그르다를 따질 수 있는 유의 수준이 결정되기 때문이다.
먼저, 귀무(영)가설의 내용이 옳은 데도 불구하고 귀무(영)가설을 기각하는 과오가 있다.
앞의 예에서 그 동전은 절묘하게 균형 있게 찌그러져 있어 진실로 앞면이 나올 확률이
0.5이라고 하자.
그럼에도 불구하고 100번을 던져 본 결과 앞면이 21번밖에 나오지 않아 귀무가설( Ho: P(앞면)=0.50)을 기각했다면 오류(과오)를 범한 것이 되는 데, 이러한 과오를 제1종과오라고 부른다.
사실, 정상적인 동전이라도 100번 중 앞면이 21번나올 수도 있기 때문에 이러한 제1종과오를 범할 확률을 유의수준(significance level)이라고 부르며, α로 표시한다.
일반적으로 α=0.05(5%)를 사용한다.
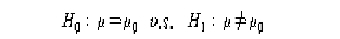
을 가설검증 한다고 하자.
여기서 μo는 어떤 주어진 값을 나타내는 데 상식적으로 표본평균 값이 μo와 너무 큰 차이가 난다면
Ho를 기각하게 될 것이다.
그러면 귀무가설(영가설)이 맞는다라는 가정 하에서 검증통계량 의 분포를 얻어 보면 그 분포는
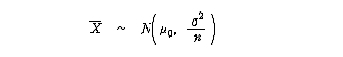
가 된다. [그림 6-1]에서 보는 바와 같이 모집단의 평균이 μ이더라도 표본평균의 값들은 아주 작은 값에서 아주 큰 값까지 얻어질 수가 있다.
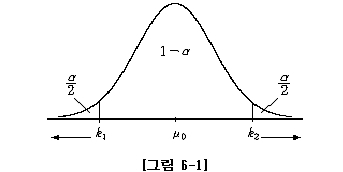
만일 표본평균값이 k1보다 작거나 또는 k2보다 클 경우 그 표본평균값은 μo와 너무 큰 차이가 나는 것이므로 설령 모집단의 평균이 μo라 할지라도 귀무가설(Ho)를 기각하는 의사결정을 내릴 수밖에 없다.
다시 말하면, 그러한 의사결정을 내릴 수밖에 없는 범위에 해당되는 확률을 유의수준(α)이라고 부르는데, 이 값이 주어져야 k1과 k2 값이 정해질 것이며 표본 평균값이 k1보다 작거나 k2보다 클 때 Ho를 기각한다는 것이다.

'품질 > 통계' 카테고리의 다른 글
| 통계꽁트1 (0) | 2022.11.15 |
|---|---|
| 통계기초17:제1종의 오류 (0) | 2022.11.11 |
| 통계기초15:가설검증 (0) | 2022.11.10 |
| 통계기초14:추정(구간추정) (0) | 2022.11.10 |
| 통계기초13:추정(점추정) (0) | 2022.11.10 |
