5-2 구간추정......너무도 중요하다....
일상생활에서 확실히 알지 못하는 어떤 값에 대한 표현으로 「어떤 정도이다」라고 한다.
이를테면, 어느 전시장의 시간당 입장객 수는 40~50명 정도라고 하거나, 그 회사 임원들 연봉이 5000~6000만원 정도 된다고 한다.
이렇게 (모집단에 대해서) 모르는 어떤 값(파라메터)을 추정하는 데 있어 하나의 값으로 추정하는 것이 아니고 구간으로 추정하는 것을 구간추정이라고 한다.
이와 같이 모집단의 파라메터를 추정함에 있어 표본으로부터 얻어진 하나의 값으로 추정을 하는 것(점추정)보다는 그 파라메터가 어느 구간 내에 들어 있을 것으로 표현(추정)하는 것이 더 적절한 경우가 있을 것이다.
예를 들어, 어느 제품의 시장점유율이 37%라고 점추정하는 것보다는 (35%, 39%)내에 있다고 표현하는 것이 필요한 경우이다.
구간추정(interval estimation)이란 신뢰수준(신뢰확률, 신뢰도)이 일정하게 주어지고 파라메터가 들어 있는 구간을 찾는 작업을 말한다.
그러면 신뢰수준이라는 것은 왜 필요한가?
예를 들어, 현재 타고 있는 전철 1량 내에 들어 있는 사람들의 평균 연령은 어떤 구간 내에 있을까를 추정한다고 할 때 [10세, 70세]으로 추정한다면 추정의 의미가 상실된다.
왜냐하면, 평균연령이 10세 이상이고 70세 이하일 것은 당연하기 때문이다.
다시 말하면, 평균연령이 [10세, 70세] 범위 내에 있다는 것은 100% 믿을 수 있다는 말이다.
그러므로, 구간추정을 하고자 할 경우 그 구간의 폭은 어느 정도까지로 한정되어야 하며, 그 결과를 신뢰할만한 수준 또한 결정되어야 한다는 것이다.
신뢰수준으로서 95%를 사용하는 것이 일반적이지만 꼭 95%이어야만 하는 것은 아니다. 신뢰수준을 로 한다면 신뢰구간의 폭이 95%일 때보다는 넓어지게 된다.
5-3 평균(μ)에 대한 신뢰구간 추정
모집단의 평균에 대한 구간추정을 한다고 할 때 표본평균 (X바)를 도구로 삼아야 하는 것은 당연하다.
왜냐하면 앞 절에서 설명한 바와 같이 X바를 점추정할 때 (μ)가 가장 적합하기 때문이다. 그러면,
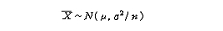
인 사실을 이용하여 (1-α)100% 신뢰수준에서의 신뢰구간을 얻어보기로 하자.
먼저, 분포를 표준화하면
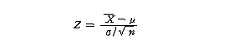
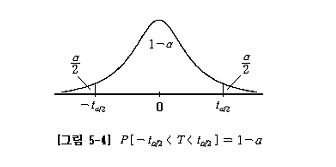
인데, 표준화정규분포 변수 Z의 분포에 대해 그림과 같이 (1-α)를 정(正) 가운데 할당하면 [그림 5-2]와 같다.
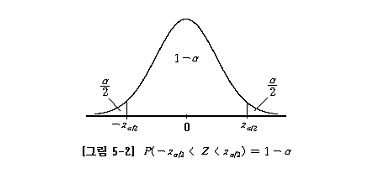
이제, [그림 5-2]를 식으로 나타내 보면,
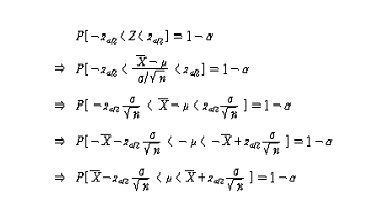
가 된다.
그러므로 μ에 대한 (1-α)100% 신뢰수준의 신뢰구간은
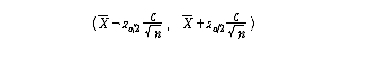
가 된다. 그러나, 이 신뢰구간은 σ값을 모르기 때문에 실제로 계산될 수가 없다. 그러므로 또한 표본으로부터 추정량을 얻어 대체해야 하는데 표본의 표준편차 (S)를 사용할 수밖에 없다. 여기서, σ대신 S를 사용해야 한다면 앞의 표준화과정에서부터 Z를 T로 바꾸어
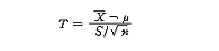
를 만들어야 하는데 T는 새로운 변수로서 자유도 (n-1)의 t-분포라고 하는 것이다.
이 t-분포의 형태는 표준화정규분포와 같이 좌우대칭이지만 표준화정규분포보다 봉우리가 낮은 분포이다.
더욱이, 자유도가 작을 때는 납작한 모양이지만, 자유도가 커질수록 봉우리가 높아진다.
확률의 분포는 t-분포표가 있는데 오른쪽 꼬리 부분의 면적에 대한 자유도별 t값을 알 수 있도록 되어있다.
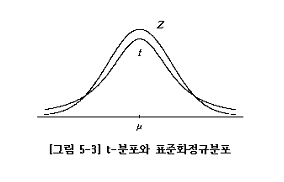
그러면, 앞의 전개과정 식들을 식(5-2), [그림 5-4]에 기초하여 전개하면 결과적으로
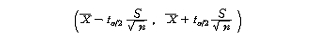
를 얻게 된다.

'품질 > 통계' 카테고리의 다른 글
| 통계기초16:유의수준 (0) | 2022.11.11 |
|---|---|
| 통계기초15:가설검증 (0) | 2022.11.10 |
| 통계기초13:추정(점추정) (0) | 2022.11.10 |
| 통계기초12:표본추출방법 (0) | 2022.11.10 |
| 통계기초11:표본평균의 분포 (0) | 2022.11.08 |

