5.추정
추정(estimation)이란 모르는 값을 추측하여 알아내는 것을 말한다.
추정이라는 개념은 장래시점의 모르는 값을 추측하여 알아내는 예측(forecast)과는 구별되어 사용되지만, 예측을 추정의 범주에 포함시켜 생각해도 무방하다.
어느 슈퍼에서 1일 평균판매액이 얼마인가를 추정한다고 할 때 어느 특정한 하루의 판매액으로 추정하는 것보다는 며칠에 걸쳐 얻어진 판매액들의 평균값으로 추정하는 것이 바람직할 것이다. 다른 예로써, 어느 초등학교 전교생 중에서 가장 키가 큰 학생은 몇 cm가 될 것인가를 알고 싶을 경우, 표본으로 50명의 학생들의 키를 얻는다고 할 때, 50명의 표본값들 중에서 가장 큰 값으로 전교생 최장신의 키를 추정할 수 있을 것이다.
이와 같이 우리는 표본으로부터 모집단의 성격을 알아내고자 하는 것이고, 이렇게 알아내고자 하는 값을 모수라고 할 때 그 모수가 무엇인가에 따라 추정하는 방법도 달라진다.
또, 모수에 대해 「어느 한 값으로 추정할 것인가?」또는, 그 모수가 「어느 구간에 들어 있을 것인가?」에 따라 점추정과 구간추정으로 나누어진다.
5-1 점추정
점추정(point estimation)이란 모집단의 모수값을 추정함에 있어 표본으로부터 얻은 통계량으로써 추정하는 것을 말한다. 즉, 모집단의 파라메터를 추정하기 위해 표본을 얻는다면 그 표본(x1, x2,...........xn)
이 될 것이고, 이 표본으로 부터 얻을 수 있는 어떤 통계량으로 추정할 것인가를 생각해야 한다. 먼저, 특정한 통계량을 추정의 목적으로 사용할 때 그 통계량을 추정량(estimator)라고 부른다. 그리고, 구체적으로 얻어진 표본값들(x1, x2,...........xn) 으로 부터 계산된 그 추정량의 구체적인 값을 추정치(estimate)라고 부른다.
모집단의 평균(뮤)을 추정하기 위한 추정량(통계량)은 무수히 많은데 어떤 추정량이 바람직한 추정량인가를 살펴보자.
모집단의 평균(뮤)을 추정하기 위해서는 표본평균 (X바)가 가장 좋은 추정량이라는 것이다.
그러나, 실제로는 하나의 표본, 에서 계산된 표본평균값(X바) 로써 (뮤)를
추정한다는 것인데 표본의 크기가 매우 크다면 표본평균값(X바)은 (뮤)의 근처에 있게 됨을
알 수 있다.
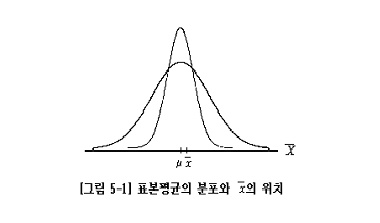
[그림 5-1]에서 N이 크면 (X바)의 분포형태가 뾰족하게 되고 실제로 얻어진 (X바의 값은
(뮤)와 가까이 위치하게 될 것임을 볼 수 있다.
극단적으로 표본크기가 무한대라면 표본평균은 곧 모집단평균이다.
여기서, (X바)의 표준편차(
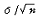
)를 표준오차(standard error)라고 부른다.
즉, 단순한 확률변수(X바)에 대해서는 표준편차, 통계량의 표준편차는 그 통계량의
표준오차라고 구분하여 부르는 것이다.
'품질 > 통계' 카테고리의 다른 글
| 통계기초15:가설검증 (0) | 2022.11.10 |
|---|---|
| 통계기초14:추정(구간추정) (0) | 2022.11.10 |
| 통계기초12:표본추출방법 (0) | 2022.11.10 |
| 통계기초11:표본평균의 분포 (0) | 2022.11.08 |
| 통계기초10:통계량 (0) | 2022.11.04 |

