-2-4 베르누이 분포
이제, 확률변수 X의 구체적인 분포의 하나인 가장 간단한 형태의 분포를 소개하기로 한다.
-- 어떤 조사나 실험에 있어 두 가지의 조사결과만이 가능한 경우가 있다.
즉, 특정인을 지지하는가, 지지하지 않는가?, 정각에 도착을 했는가 연착했는가?,
부도를 냈는가 내지 않았는가? 등등
-- 두 가지 중에 어떤 일이 일어났는가를 조사하는 경우이다. 이와 같은 경우에 어느 하나를
-- 성공이라 부르고 다른 하나를 실패라고 하자. 그러면, 변수 X는

로 표현되는데 이와 같은 확률변수는 베르누이(Bernoulli) 분포한다고 한다.
-- 좀더 구체적으로 설명하면
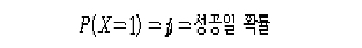
라 할 경우, X는

의 분포에 따른다고 한다.
-- 베르누이분포는 백분비(비율)로 얻어지는 자료를 다루는데 필요한 분포이다. 예를 들면,
-- A회사 제품의 시장점유율이 40%라고 하자. 전체시장(모집단)의 구성원 각각이 A제품 고객인가
-- 아닌가를 나타내기 위해서 변수 X를

로 하면

이며, X의 확률분포는

이 되는 것이다.

이다.
2-5 정규분포
우리 주위의 많은 자료(변수)들은 정규분포를 한다고 해도 과언이 아니다. 실제로 어떤 변수에
-- 대해 많은 수의 데이터를 얻었을 경우, 그 자료들의 그래프를 얻어 보면 정규분포라는 분포에
-- 가까운 것을 알 수 있다. 더욱이, 거의 모든 통계이론이 정규분포를 배경으로 이루어져 있기
-- 때문에 정규분포를 이해하는 것은 매우 중요한 일이다.
-- 우선 정규분포는 평균을 중심으로 좌우대칭이다. 그리고 퍼짐의 정도는 표준편차로 나타낼
-- 수 있는데, 분포 모양은 [그림 2-4]와 같다.

정규분포하는 변수의 확률분포는 바로 [그림 2-4]의 곡선의 형태인데, 이는

이다. 물론 모집단 자료들의 분포형태가 [그림 2-4]와 같고 모집단의 평균과 표준편차의
-- 크기에 따라 정규분포의 모양은 상당히 뾰족할 수도 있고 납작한 형태의 펑퍼짐한 형태일
-- 수도 있다.
[그림 2-5]는 여러 가지 형태의 정규분포를 나타내고 있는데, [그림 2-5(A)]는
-- 평균은 같은데 표준편차가 다른 경우이고, [그림 2-5(B)]는 표준편차는 같은데 평균이 다른
-- 경우이다.

또한 베르누이 분포에서는 f(x)가 그 자체로서 확률을 나타내지만 연속적인 변수의 하나인
-- 정규분포에서는 f(x)가 [그림 2-4]의 곡선식이지 그 자체가 확률을 나타내는 것은 아니다.
-- 따라서 정규분포에서의 확률은 곡선 아래 부분의 면적을 구하는 것과 같은데, 확률을 구하기
-- 위해 어떤 정규분포이든지 표준화(standardization)를 시켜 표준화된 정규분포로 바꾸면 된다.
'품질 > 통계' 카테고리의 다른 글
| 기초통계9:표본이론 (0) | 2022.11.04 |
|---|---|
| 기초통계8:표준정규분포 (0) | 2022.11.04 |
| 기초통계6:기대값 (0) | 2022.11.03 |
| 기초통계5:확률분포 (0) | 2022.11.03 |
| 기초통계4:확률분포 (1) | 2022.11.03 |



